【教育版マインクラフト】4-6 チェス盤のような格子模様にブロックを置く

普通に作ると少しタイヘン・・・
今回はチェス盤のように格子模様にブロックを置くプログラムを解説します。
全体的な流れは、2つの変数(num1とnum2)を使って、条件に基づいてブロックを配置する処理を行っています。主な処理の流れとしては行の方向と列の方向でそれぞれの番号が奇数か偶数かを判定して黒いブロックか白いブロックのどちらかを置いていくものです。しかし、これだと少し複雑でわかりにくいコードです。
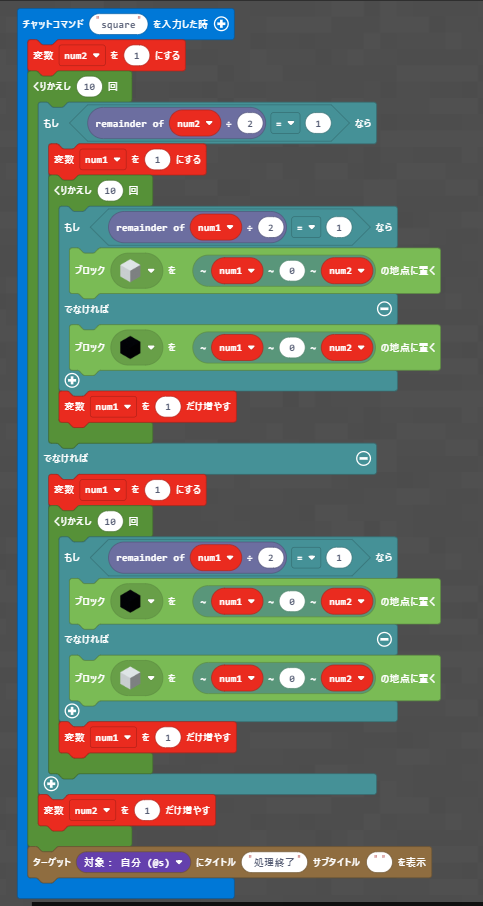

もう少し工夫を
少しプログラムが長いので短くしてみましょう。まずはブロックを置く前に原理的な部分を把握するコードを作ってみます。
このプログラムは、指定された回数(num1 と num2 の値に基づく)繰り返し処理を行い、変数「タテ」と「ヨコ」の足した結果をメッセージとして送信しながら、繰り返しごとに「ヨコ」を増加させていきます。
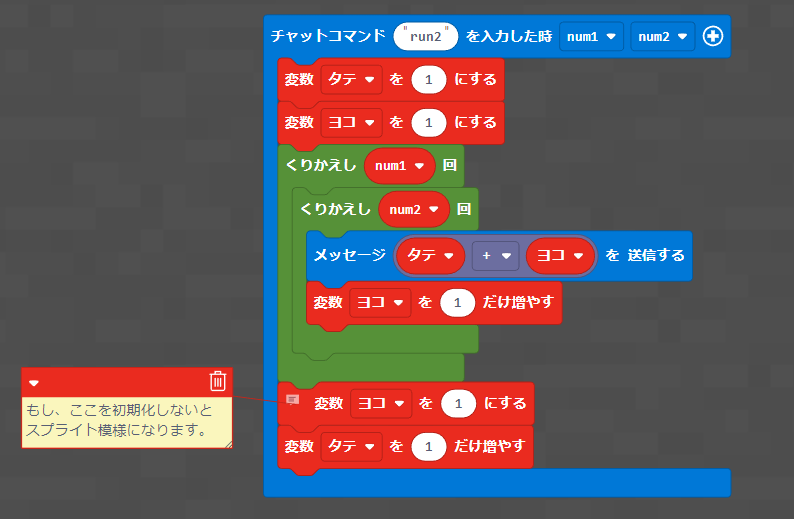
プログラムの流れ:
- 初期化:
- 変数「タテ」を 1 に設定します。
- 変数「ヨコ」を 1 に設定します。
- 外側のループ:
- 「num1」の値の回数だけ繰り返し処理を行います。
- 内側のループ:
- 「num2」の値の回数だけ繰り返し処理を行います。
- そのたびに、「タテ」と「ヨコ」の和の値をメッセージとして送信します。
- 変数「ヨコ」の値を1ずつ増やします。
- 次の外側ループへ:
- 内側のループが終了した後、「ヨコ」を再び1にリセットします。
- 「タテ」の値を1ずつ増やします。
次にブロックを置く処理を追加する:
上記のプログラムは奇数列と偶数列、奇数行と偶数行を組み合わせて場合分けをする処理となります。
「黒を置くか白を置くか」は二重ループの変数タテ,ヨコの単純な計算式((タテ+ヨコ)%2=0か否か)で判断できますので今回はこれを使ってみましょう。なお通常はカウンター変数はiやjを使うことも多いです。
たとえば5×5のマスを考え、そこに行番号と列番号の和を書いてみましょう。すると、それが奇数か偶数かで格子模様に分けることができることに気づくかと思います。
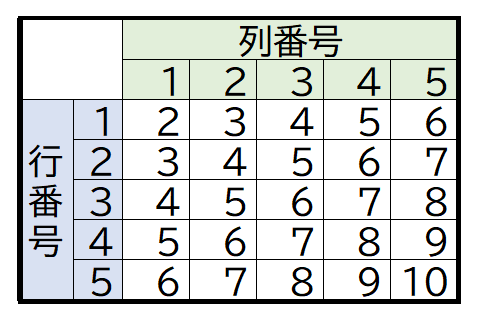
コードをただ漫然と写すのではなく、各ループの変数の初期化や加算の処理をよく注意して追いましょう。また先ほどのようにまずはブロックを置く処理を書く前に数値だけを出力するプログラムを作って全体像を把握し、骨組みからより詳細に作るのも一つの方法です(段階的詳細化)。
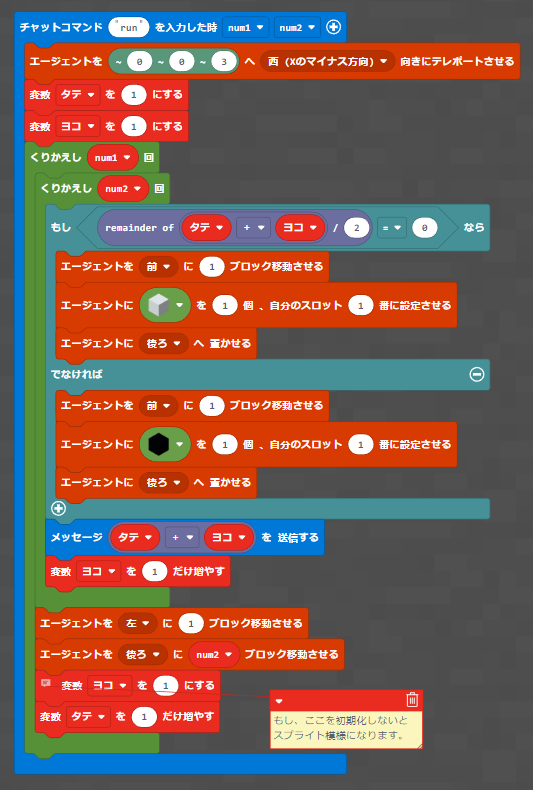
プログラムの流れ:
- 初期設定:
- エージェントを特定の座標にテレポートさせます。
- 変数「タテ」と「ヨコ」を 1 にリセットします。
- 外側のループ:
- 「num1」の回数分、繰り返し処理を行います。
- 内側のループ:
- 「num2」の回数分、繰り返し処理を行います。
- 「タテ」と「ヨコ」の余り(mod)が2で割り切れる場合:
- エージェントが前に進んで、後ろに白いブロックを置く処理を実行します。
- もし余りが2で割り切れない場合:
- エージェントが前に進んで、後ろに黒いブロックを置く処理を実行します。
- メッセージ送信:
- 「タテ」と「ヨコ」の値をメッセージとして送信します(確認用なので)。
- 変数の増加:
- 「ヨコ」の値を1増やします。
- 内側のループが終わったら、エージェントを移動させる:
- エージェントを左に動かし、ブロックを別の場所に移動させます。
- 「ヨコ」を1にリセットし、「タテ」を1増やします。

いくつか例に示したように書き方は行く通りもあり、丸暗記ではとうてい無理です。
大切なのはコードの意味を理解する(仕組みを自分の言葉で言い直すことができる)ことです。
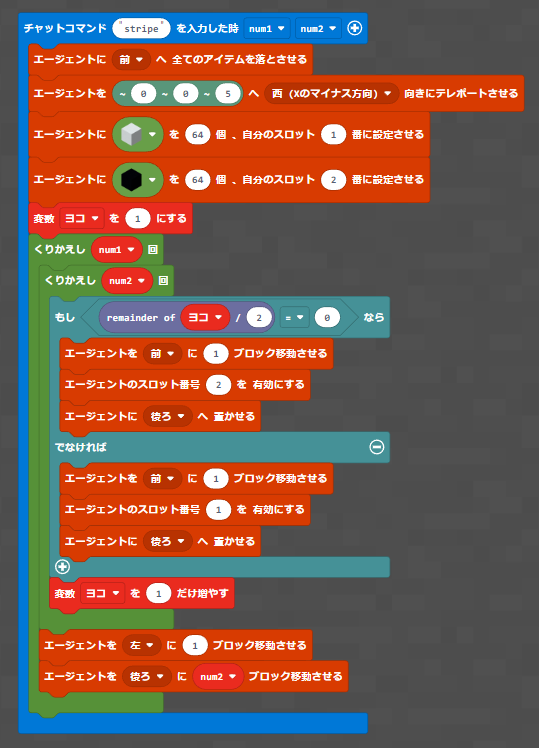
オマケ:ストライプ模様を作る
ストライプ模様はこの応用で作ることができます。こちらは、変数の「タテ」の部分は同じブロックのまま配置し、「ヨコ」の値が偶数か奇数かによって、配置するブロックが変わるのが特徴です。

コース・WEB講座
目次へ戻る
教育版マインクラフト・プログラミング入門
マインクラフトコースについてはこちら
https://tsukurium.net/kitaurawa-minecraft-club/
体験会開催中です。
当教室では教育版マインクラフトコース開講中です。
先生のお話がしっかり聞くことができ、ルールを守れる人なら年長さんからでも入会可能です。
また当教室のマインクラフトコースはよくあるような既存の学びに対するカウンターカルチャーや逃避の場を志向するものではなく、教育版マインクラフトの特徴を活かしつつ高校の情報Ⅰや大学入試などメインストリームのしっかりとした学びにつながるものを志向するものです。
お問いあわせ・ご入会・体験会のお申込みは下記のリンクからお願いいたします。
画像をクリックするとお問い合わせページにジャンプします。


